\( \newcommand\al{\alpha} \newcommand\be{\beta} \newcommand\de{\delta} \newcommand\De{\Delta} \newcommand\eps{\epsilon} \newcommand\ga{\gamma} \newcommand\Ga{\Gamma} \newcommand\ka{\kappa} \newcommand\la{\lambda} \newcommand\La{\Lambda} \newcommand\om{\omega} \newcommand\Om{\Omega} \newcommand\sg{\sigma} \newcommand\Sg{\Sigma} \renewcommand\th{\theta} %--- Latex uses \th for a Norse character \newcommand\Th{\Theta} \newcommand\vphi{\varphi} % % some calligraphy % \newcommand\cA{{\mathcal A}} \newcommand\cB{{\mathcal B}} \newcommand\cC{{\mathcal C}} \newcommand\cD{{\mathcal D}} \newcommand\cE{{\mathcal E}} \newcommand\cF{{\mathcal F}} \newcommand\cG{{\mathcal G}} \newcommand\cH{{\mathcal H}} \newcommand\cI{{\mathcal I}} \newcommand\cJ{{\mathcal J}} \newcommand\cK{{\mathcal K}} \newcommand\cL{{\mathcal L}} \newcommand\cM{{\mathcal M}} \newcommand\cN{{\mathcal N}} \newcommand\cO{{\mathcal O}} \newcommand\cP{{\mathcal P}} \newcommand\cQ{{\mathcal Q}} \newcommand\cR{{\mathcal R}} \newcommand\cS{{\mathcal S}} \newcommand\cT{{\mathcal T}} \newcommand\cU{{\mathcal U}} \newcommand\cV{{\mathcal V}} % % fields and rings (and a semigroup) % \newcommand\cx{{\mathbb C}}% complexes \newcommand\fld{{\mathbb F}} \newcommand\flde{{\mathbb E}} \newcommand\ints{{\mathbb Z}} \newcommand\nn{{\mathbb N}}%non-negative integers \newcommand\re{{\mathbb R}}%reals \newcommand\rats{{\mathbb Q}} % % the really useful stuff % \newcommand\comp[1]{{\mkern2mu\overline{\mkern-2mu#1}}} \newcommand\diff{\mathbin{\mkern-1.5mu\setminus\mkern-1.5mu}}% for \setminus \newcommand\res{\mathbin{\mkern-2.0mu\restriction\mkern-2.0mu}} \newcommand\sbs{\subseteq} \newcommand\sps{\supseteq} \newcommand\seq[3]{#1_{#2},\ldots,#1_{#3}} \DeclareMathOperator{\supp}{supp} \DeclareMathOperator{\im}{im} \DeclareMathOperator{\row}{row} \newcommand\pmat[1]{\begin{pmatrix} #1 \end{pmatrix}} \newcommand\cprod{\mathbin{\square}} \newcommand\gbin[2]{\genfrac{[}{]}{0pt}{}{#1}{#2}} % % matrix theory % \newcommand\ip[2]{\langle#1,#2\rangle} \newcommand\one{{\bf1}} \DeclareMathOperator{\rk}{rk} \DeclareMathOperator{\tr}{tr} \DeclareMathOperator{\col}{col} \newcommand\mat[3]{\mathrm{Mat}_{#1\times #2}(#3)} \newcommand\sm[3]{\sum_{#1=#2}^{#3}} % % some group theory % \newcommand\aut[1]{{\rm Aut}(#1)} \newcommand\fx[1]{{\rm fix}(#1)}% ch2 \newcommand\grp[1]{\langle #1\rangle} \newcommand\nrml{\vartriangleleft} \newcommand\nrmleq{\trianglelefteq} \DeclareMathOperator{\Sym}{Sym} \newcommand\sym[1]{\Sym(#1)} \DeclareMathOperator{\Alt}{Alt} \newcommand\alt[1]{\Alt(#1)} \)

Chapter5One-Factors of \(K_6\)

Robert A. Beezer

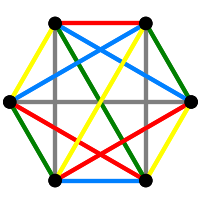
In this chapter, we start with the complete graph on six vertices, \(K_6\) and begin to construct three diverse and remarkable combinatorial structures. This material follows Chapter 6, “A property of the number six” of “Designs, Graphs, Codes and their Links” by P.J. Cameron and J.H. van Lint, who in turn credit lectures of G. Higman. We begin with the vertices and edges of the complete graph, and then create sets of three disjoint edges known as \(1\)-factors. Collections of \(1\)-factors become factorizations of the original complete graph. Vertices, edges, factors and factorizations then all combine in Chapter 6 to create our three ultimate combinatorial structures.