\( \newcommand\al{\alpha} \newcommand\be{\beta} \newcommand\de{\delta} \newcommand\De{\Delta} \newcommand\eps{\epsilon} \newcommand\ga{\gamma} \newcommand\Ga{\Gamma} \newcommand\ka{\kappa} \newcommand\la{\lambda} \newcommand\La{\Lambda} \newcommand\om{\omega} \newcommand\Om{\Omega} \newcommand\sg{\sigma} \newcommand\Sg{\Sigma} \renewcommand\th{\theta} %--- Latex uses \th for a Norse character \newcommand\Th{\Theta} \newcommand\vphi{\varphi} % % some calligraphy % \newcommand\cA{{\mathcal A}} \newcommand\cB{{\mathcal B}} \newcommand\cC{{\mathcal C}} \newcommand\cD{{\mathcal D}} \newcommand\cE{{\mathcal E}} \newcommand\cF{{\mathcal F}} \newcommand\cG{{\mathcal G}} \newcommand\cH{{\mathcal H}} \newcommand\cI{{\mathcal I}} \newcommand\cJ{{\mathcal J}} \newcommand\cK{{\mathcal K}} \newcommand\cL{{\mathcal L}} \newcommand\cM{{\mathcal M}} \newcommand\cN{{\mathcal N}} \newcommand\cO{{\mathcal O}} \newcommand\cP{{\mathcal P}} \newcommand\cQ{{\mathcal Q}} \newcommand\cR{{\mathcal R}} \newcommand\cS{{\mathcal S}} \newcommand\cT{{\mathcal T}} \newcommand\cU{{\mathcal U}} \newcommand\cV{{\mathcal V}} % % fields and rings (and a semigroup) % \newcommand\cx{{\mathbb C}}% complexes \newcommand\fld{{\mathbb F}} \newcommand\flde{{\mathbb E}} \newcommand\ints{{\mathbb Z}} \newcommand\nn{{\mathbb N}}%non-negative integers \newcommand\re{{\mathbb R}}%reals \newcommand\rats{{\mathbb Q}} % % the really useful stuff % \newcommand\comp[1]{{\mkern2mu\overline{\mkern-2mu#1}}} \newcommand\diff{\mathbin{\mkern-1.5mu\setminus\mkern-1.5mu}}% for \setminus \newcommand\res{\mathbin{\mkern-2.0mu\restriction\mkern-2.0mu}} \newcommand\sbs{\subseteq} \newcommand\sps{\supseteq} \newcommand\seq[3]{#1_{#2},\ldots,#1_{#3}} \DeclareMathOperator{\supp}{supp} \DeclareMathOperator{\im}{im} \DeclareMathOperator{\row}{row} \newcommand\pmat[1]{\begin{pmatrix} #1 \end{pmatrix}} \newcommand\cprod{\mathbin{\square}} \newcommand\gbin[2]{\genfrac{[}{]}{0pt}{}{#1}{#2}} % % matrix theory % \newcommand\ip[2]{\langle#1,#2\rangle} \newcommand\one{{\bf1}} \DeclareMathOperator{\rk}{rk} \DeclareMathOperator{\tr}{tr} \DeclareMathOperator{\col}{col} \newcommand\mat[3]{\mathrm{Mat}_{#1\times #2}(#3)} \newcommand\sm[3]{\sum_{#1=#2}^{#3}} % % some group theory % \newcommand\aut[1]{{\rm Aut}(#1)} \newcommand\fx[1]{{\rm fix}(#1)}% ch2 \newcommand\grp[1]{\langle #1\rangle} \newcommand\nrml{\vartriangleleft} \newcommand\nrmleq{\trianglelefteq} \DeclareMathOperator{\Sym}{Sym} \newcommand\sym[1]{\Sym(#1)} \DeclareMathOperator{\Alt}{Alt} \newcommand\alt[1]{\Alt(#1)} \)

Section2.1Pseudosimilar Vertices

Vertices \(u\) and \(v\) in a graph \(X\) are similar if there is an automorphism of \(X\) that maps \(u\) to \(v\). If \(u\) and \(v\) are similar, then the vertex-deleted subgraphs \(X\diff u\) and \(X\diff v\) are isomorphic. If \(X\diff u\) and \(X\diff v\) are isomorphic but \(u\) and \(v\) are not similar, we say that they are pseudosimilar. It is not obvious that pairs of pseudosimilar vertices exist, but we will see that they do.

The vertex set of \(C9\) is \(\{0,\ldots,8\}\). We want to add three new vertices to \(C9\), adjacent to \(1\), \(4\) and \(7\) in turn and delete the vertex \(0\).

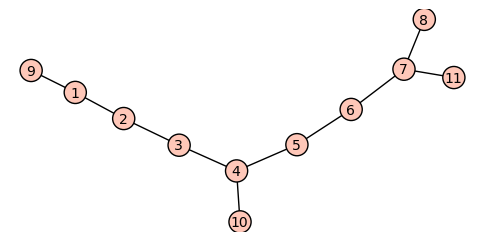
Here's \(D\):

Figure2.1.1Graph with pseudosimilar vertices.

The automorphism group of \(D\) has order 2:

and we can determine its orbits:

As an alternative to the last command we can also use

I claim \(D\) has a pair of pseudosimilar vertices. In this case we could find them by inspecting our drawing of \(D\), but we work through a general approach. The idea is to find a canonical label for each of the 11 vertex-deleted subgraphs of \(D\). The sage command

returns a canonized form of \(D\). So graphs \(G\) and \(H\) are isomorphic if and only if their canonized forms are equal. For example

The only problem left is that the return value of canonical_label() is not hashable. We can circumvent this as follows.

The following procedure constructs a hashable canonical label for \(G\diff i\), given \(G\) and \(i\).

We can now construct our list of pairs of the form (string, vertex):

and on inspecting the output, we see that \(D\diff 3\cong D\diff 6\), which we can also ask Sage to do for us instead via a one-line list comprehension,

As an exercise, construct a graph on 8 vertices with a pair of pseudosimilar vertices.

Now we describe how to get a list of the sets of vertices such that all vertices in the same set have the same vertex-deleted subgraphs. First we need to convert our list of pairs to a dictionary keyed on the first term of the pair; the value of a key will be all second terms with the same first term. (The keys for a dictionary must be hashable, so this is why we needed the graph6 strings.)

Now if dc is a dictionary whose values are lists, we compute a list consisting of those values whose length is at least \(k\):

We apply this to our list labels:

We see again that 3 and 6 form a pseudosimilar pair of vertices.

For further reading on pseudosimilar vertices, you will have to dig out papers on the topic. I suspect that few of these are on the web, since they predate \(\mathrm{\LaTeX}\). Fortunately we still have libraries. Note that pseudosimilar sets of size greater than two are possible.